In this blog post we will try to cover the following questions:
- What’s the bias-variance trade-off?
- How’s this tradeoff related to overfitting and underfitting?
- How do you know that your model is high variance, low bias? What would you do in this case?
- How do you know that your model is low variance, high bias? What would you do in this case?
The central goal of (supervised) Machine learning is to find models that are able to generalize to new unseen data. i.e predicting behaviour under new conditions. In practice we use error measures to get an estimate of a model's generalization capability. i.e finding out how well our model will perform on instances it has never seen before. We first split our given dataset into train and test set (consisting of examples that were collected separately from the training set). We make an assumption that the examples in each dataset are independent from each other, and that the training set and test set are identically distributed , drawn from the same probability distribution as each other.
Then, training error measures the error on the training data, minimizing which is an optimization problem. We can estimate the generalization error of a machine learning model by measuring its performance on a test set. Formally, generalization error (or test error), measures the expected error on new input data (new cases). For example when our learner outputs a classifier that is 100% accurate on the training data but only 50% accurate on test data, we say it has overfit the training set.
The factors determining how well a machine learning algorithm will perform are its ability to:
- Make the training error small.
- Make the gap between training and test error small
These two factors correspond to the two central challenges in machine learning: underfitting and overfitting. Underfitting occurs when the model is not able to obtain a sufficiently low error value on the training set. Overfitting occurs when the gap between the training error and test error is too large. We say a model has low Bias because it fits the training data well, but high Variance because it does a bad job withnew unseen Data.
To better understand generalization error from a practical perspective, we can decompose the generalization error into bias and variance:
High Bias: If its not fitting the training set well (as shown by the train set error) then algorithm is said to have high bias. A high bias model tends to be too simplistic and fails to capture the underlying structure of the data.This may occur for example if we have overly simplistic assumptions about the relationship between the input variables and the target variable, leading to underfitting of the training data and poor performance on new data. In practice we can look at the train set error and dev set error.
High Variance: When a learning algorithm outputs a prediction function with generalization error much higher than its training error i.e gap between the training error and test error is too large, then it is said to have overfit the training data. This maybe because the model is too complex and overfits to the noise and randomness in the training data.
Bias vs. Variance tradeoff: Of the changes we could make to most learning algorithms, there are some that reduce bias errors but at the cost of increasing variance, and vice versa. This creates a “trade off” between bias and variance. For example, increasing the size of your model—adding neurons/layers in a neural network, or adding input features—generally reduces bias but could increase variance. Alternatively,adding regularization generally increases bias but reduces variance.
Model Capacity: The goal is to find a model that balances bias and variance to make accurate predictions on new data. In practice, during our experiments, our challenge is to choose a model with the right 'capacity'. A model’s capacity measures the range of functions it can fit. This means we should pick machine learning models that match the complexity of task to be solved and the training data available. e.g quadratic model will generalize well if the underlying function is quadratic. During experimentation, we have the option to alter the hypothesis space i.e the set of functions that the learning algorithm is allowed to select as being the solution. Machine learning algorithms will generally perform best when their capacity is appropriate for the true complexity of the task they need to perform and the amount of training data they are provided with. Models with insufficient capacity are unable to solve complex tasks. Models with high capacity can solve complex tasks, but when their capacity is higher than needed to solve the task at hand, they may overfit.
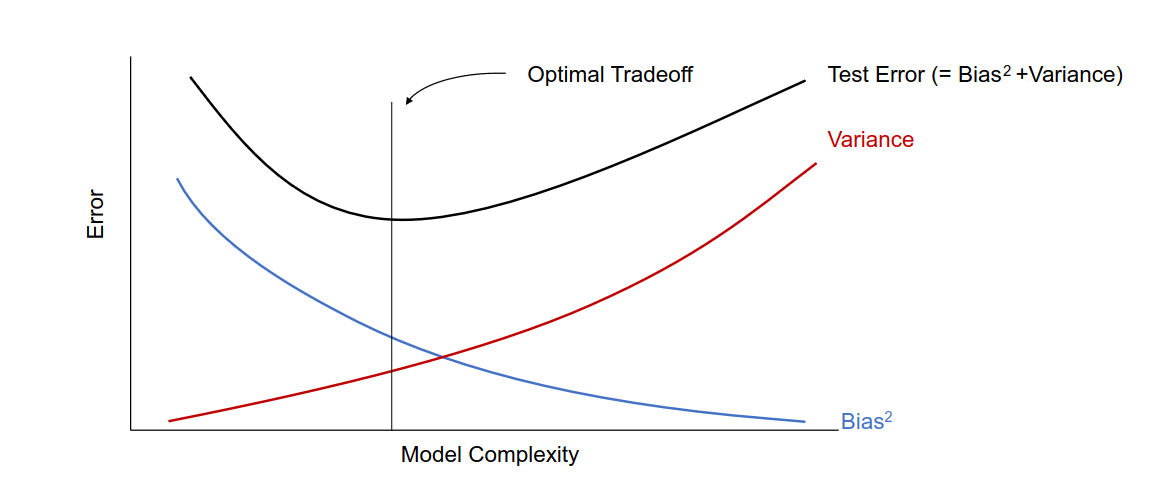
In first figure, The test error can be decomposed as a summation of bias and variance. As model capacity increases, bias tends to decrease, while variance tends to increase. This means that the test error will have a convex curve as the model complexity increases, and in practice we should tune the model complexity to achieve the best tradeoff. The optimal model is the one that balances the bias and variance, leading to low error on both the training and testing data.
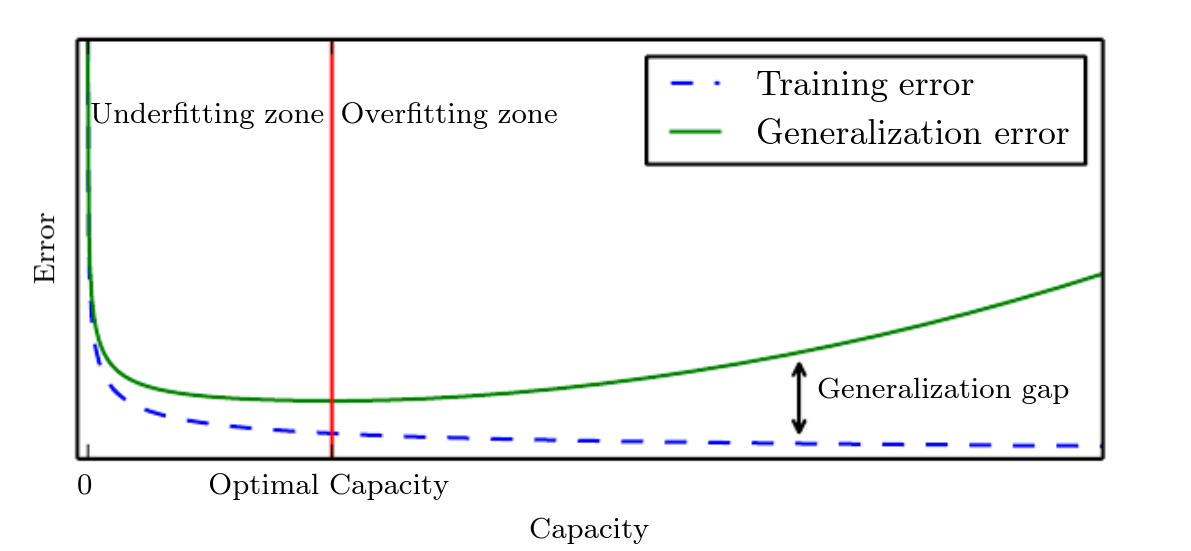
2nd Figure: Typically, training error decreases until it asymptotes to the minimum possible error value as model capacity increases (assuming the error measure has a minimum value). Generalization error has a U-shaped curve as a function of model capacity. In the 2nd figure, on the left end of the graph, training error and generalization error are both high. This is the underfitting regime and as we increase capacity, training error decreases, but the gap between training and generalization error increases. Eventually, the size of this gap outweighs the decrease in training error, and we enter the overfitting regime, where capacity is too large, above the optimal capacity.
References:
- Few useful things to know about ML
- Deep Learning Book - Chapter 5
- Machine Learning Yearning
- https://cs229.stanford.edu/notes2022fall/main_notes.pdf
